O conceito de esfera
A esfera no espaço R³ é uma superfície muito importante em função de suas aplicações a problemas da vida. Do ponto de vista matemático, a esfera no espaço R³ é confundida com o sólido geométrico (disco esférico) envolvido pela mesma, razão pela qual muitas pessoas calculam o
volume da esfera. Na maioria dos livros elementares sobre Geometria, a esfera é tratada como se fosse um sólido, herança da Geometria Euclidiana.
Embora não seja correto, muitas vezes necessitamos falar palavras que sejam entendidas pela coletividade. De um ponto de vista mais cuidadoso, a esfera no espaço R³ é um objeto matemático parametrizado por duas dimensões, o que significa que podemos obter medidas de área e de comprimento mas o volume tem medida nula. Há outras esferas, cada uma definida no seu respectivo espaço n-dimensional. Um caso interessante é a esfera na reta unidimensional:
S
o = {x em R: x²=1} = {+1,-1}
Por exemplo, a esfera
S
1 = { (x,y) em R²: x² + y² = 1 }
é conhecida por nós como uma circunferência de raio unitário centrada na origem do plano cartesiano.
Aplicação: volumes de líquidos
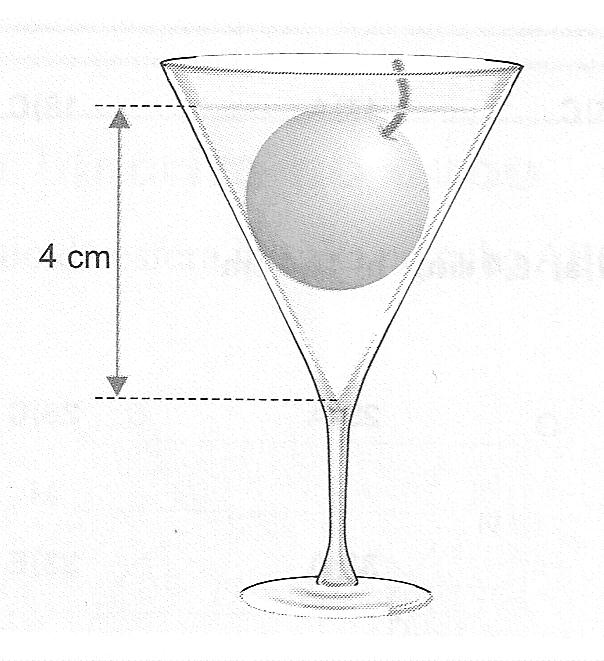
Um problema fundamental para empresas que armazenam líquidos em tanques esféricos, cilíndricos ou esféricos e cilíndricos é a necessidade de realizar cálculos de volumes de regiões esféricas a partir do conhecimento da altura do líquido colocado na mesma. Por exemplo, quando um tanque é esférico, ele possui um orifício na parte superior (polo Norte) por onde é introduzida verticalmente uma vara com indicadores de medidas. Ao retirar a vara, observa-se o nível de líquido que fica impregnado na vara e esta medida corresponde à altura de líquido contido na região esférica. Este não é um problema trivial, como observaremos pelos cálculos realizados na sequência.
A seguir apresentaremos elementos esféricos básicos e algumas fórmulas para cálculos de áreas na esfera e volumes em um sólido esférico.
A superfície esférica
A esfera no espaço R³ é o conjunto de todos os pontos do espaço que estão localizados a uma mesma distância denominada raio de um ponto fixo chamado centro.
Uma notação para a esfera com raio unitário centrada na origem de R³ é:
S² = { (x,y,z) em R³: x² + y² + z² = 1 }
Uma esfera de raio unitário centrada na origem de R
4 é dada por:
S³ = { (w,x,y,z) em R
4: w² + x² + y² + z² = 1 }
Você conseguiria imaginar espacialmente tal esfera?
Do ponto de vista prático, a esfera pode ser pensada como a película fina que envolve um sólido esférico. Em uma melancia esférica, a esfera poderia ser considerada a película verde (casca) que envolve a fruta.
É comum encontrarmos na literatura básica a definição de esfera como sendo o sólido esférico, no entanto não se deve confundir estes conceitos. Se houver interesse em aprofundar os estudos desses detalhes, deve-se tomar algum bom livro de Geometria Diferencial que é a área da Matemática que trata do detalhamento de tais situações.
O disco esférico é o conjunto de todos os pontos do espaço que estão localizados na casca e dentro da esfera. Do ponto de vista prático, o disco esférico pode ser pensado como a reunião da película fina que envolve o sólido esférico com a região sólida dentro da esfera. Em uma melancia esférica, o disco esférico pode ser visto como toda a fruta.
Quando indicamos o raio da esfera pela letra R e o centro da esfera pelo ponto (0,0,0), a equação da esfera é dada por:
x² + y² + z² = R²
e a relação matemática que define o disco esférico é o conjunto que contém a casca reunido com o interior, isto é:
x² + y² + z²
< R²
Quando indicamos o raio da esfera pela letra R e o centro da esfera pelo ponto (x
o,y
o,z
o), a equação da esfera é dada por:
(x-x
o)² + (y-y
o)² + (z-z
o)² = R²
e a relação matemática que define o disco esférico é o conjunto que contém a casca reunido com o interior, isto é, o conjunto de todos os pontos (x,y,z) em R³ tal que:
(x-x
o)² + (y-y
o)² + (z-z
o)²
< R²
Da forma como está definida, a esfera centrada na origem pode ser construída no espaço euclidiano R³ de modo que o centro da mesma venha a coincidir com a origem do sistema cartesiano R³, logo podemos fazer passar os eixos OX, OY e OZ, pelo ponto (0,0,0).
Seccionando a esfera x²+y²+z²=R² com o plano z=0, obteremos duas superfícies semelhantes: o hemisfério Norte ("boca para baixo") que é o conjunto de todos os pontos da esfera onde a cota z é não negativa e o hemisfério Sul ("boca para cima") que é o conjunto de todos os pontos da esfera onde a cota z não é positiva.
Se seccionarmos a esfera x²+y²+z²=R² por um plano vertical que passa em (0,0,0), por exemplo, o plano x=0, teremos uma circunferência maximal C da esfera que é uma circunferência contida na esfera cuja medida do raio coincide com a medida do raio da esfera, construída no plano YZ e a equação desta circunferência será:
x=0, y² + z² = R
2
sendo que esta circunferência intersecta o eixo OZ nos pontos de coordenadas (0,0,R) e (0,0,-R). Existem infinitas circunferências maximais em uma esfera.
Se rodarmos esta circunferência maximal C em torno do eixo OZ, obteremos a esfera através da rotação e por este motivo, a esfera é uma superfície de revolução.
Se tomarmos um arco contido na circunferência maximal cujas extremidades são os pontos (0,0,R) e (0,p,q) tal que p²+q²=R² e rodarmos este arco em torno do eixo OZ, obteremos uma superfície denominada calota esférica.
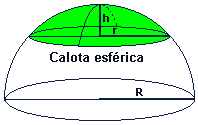
Na prática, as pessoas usam o termo calota esférica para representar tanto a superfície como o sólido geométrico envolvido pela calota esférica. Para evitar confusões, usarei "calota esférica" com aspas para o sólido e sem aspas para a superfície.
A partir da rotação, construiremos duas calotas em uma esfera, de modo que as extremidades dos arcos sejam (0,0,R) e (0,p,q) com p²+q²=R² no primeiro caso (calota Norte) e no segundo caso (calota Sul) as extremidades dos arcos (0,0,-R) e (0,r,-s) com r²+s²=R² e retirarmos estas duas calotas da esfera, teremos uma superfície de revolução denominada zona esférica.
De um ponto de vista prático, consideremos uma melancia esférica. Com uma faca, cortamos uma "calota esférica" superior e uma "calota esférica" inferior. O que sobra da melancia é uma região sólida envolvida pela zona esférica, algumas vezes denominada zona esférica.
Consideremos uma "calota esférica" com altura h
1 e raio da base r
1 e retiremos desta calota uma outra "calota esférica" com altura h
2 e raio da base r
2, de tal modo que os planos das bases de ambas sejam paralelos. A região sólida determinada pela calota maior menos a calota menor recebe o nome de segmento esférico com bases paralelas.
No que segue, usaremos esfera tanto para o sólido como para a superfície, "calota esférica" para o sólido envolvido pela calota esférica, a letra maiúscula R para entender o raio da esfera sobre a qual estamos realizando os cálculos, V será o volume, A(lateral) será a área lateral e e A(total) será a área total.
Algumas fórmulas (relações) para objetos esféricos
| Objeto | Relações e fórmulas |
|---|
| Esfera | Volume = (4/3) Pi R³
A(total) = 4 Pi R² |
|---|
Calota esférica
(altura h, raio da base r) | R² = h (2R-h)
A(lateral) = 2 Pi R h
A(total) = Pi h (4R-h)
V=Pi.h²(3R-h)/3=Pi(3R²+h²)/6 |
|---|
Segmento esférico
(altura h, raios das bases r1>r²) | R² = a² + [(r1² -r2²-h²)/2h)]²
A(lateral) = 2 Pi R h
A(total) = Pi(2Rh+r1²+r2²)
Volume=Pi.h(3r1²+3r2²+h²)/6 |
|---|
Estas fórmulas podem ser obtidas como aplicações do Cálculo Diferencial e Integral, mas nós nos limitaremos a apresentar um processo matemático para a obtenção da fórmula do cálculo do volume da "calota esférica" em função da altura da mesma.
Volume de uma calota no hemisfério Sul
Consideremos a esfera centrada no ponto (0,0,R) com raio R.
A equação desta esfera será dada por:
x² + y² + (z-R)² = R²
A altura da calota será indicada pela letra h e o plano que coincide com o nível do líquido (cota) será indicado por z=h. A interseção entre a esfera e este plano é dado pela circunferência
x² + y² = R² - (h-R)²
Obteremos o volume da calota esférica com a altura h menor ou igual ao raio R da esfera, isto é, h pertence ao intervalo [0,R] e neste caso poderemos explicitar o valor de z em função de x e y para obter:
Para simplificar as operações algébricas, usaremos a letra r para indicar:
r² = R² - (h-R)² = h(2R-h)
A região circular S de integração será descrita por x²+y²
<R² ou em coordenadas polares através de:
0
<m
<R, 0
<t
<2Pi
A integral dupla que representa o volume da calota em função da altura h é dada por:
ou seja
Escrita em Coordenadas Polares, esta integral fica na forma:
Após realizar a integral na variável t, podemos separá-la em duas integrais:
ou seja:
Com a mudança de variável u=R²-m² e du=(-2m)dm poderemos reescrever:
Após alguns cálculos obtemos:
V
C(h) = Pi (h-R) [R² -(h-R)²] - (2/3)Pi[(R-h)³ - R³]
e assim temos a fórmula para o cálculo do volume da calota esférica no hemisfério Sul com a altura h no intervalo [0,R], dada por:
V
C(h) = Pi h²(3R-h)/3
Volume de uma calota no hemisfério Norte
Se o nível do líquido mostra que a altura h já ultrapassou o raio R da região esférica, então a altura h está no intervalo [R,2R]
Lançaremos mão de uma propriedades de simetria da esfera que nos diz que o volume da calota superior assim como da calota inferior somente depende do raio R da esfera e da altura h e não da posição relativa ocupada.
Aproveitaremos o resultado do cálculo utilizado para a calota do hemisfério Sul. Tomaremos a altura tal que: h=2R-d, onde d é a altura da região que não contém o líquido. Como o volume desta calota
vazia é dado por:
V
C(d) = Pi d²(3R-d)/3
e como h=2R-d, então para h no intervalo [R,2R], poderemos escrever ov olume da calota vazia em função de h:
V
C(h) = Pi (2R-h)²(R+h)/3
Para obter o volume ocupado pelo líquido, em função da altura, basta tomar o volume total da região esférica e retirar o volume da calota
vazia, para obter:
V(h) = 4Pi R³/3 - Pi (2R-h)²(R+h)/3
que pode ser simplificada para:
V(h) = Pi h²(3R-h)/3
Independentemente do fato que a altura h esteja no intervalo [0,R] ou [R,2R] ou de uma forma geral em [0,2R], o cálculo do volume ocupado pelo líquido é dado por:
V(h) = Pi h²(3R-h)/3
Essa questão eu achei bem interessante,porque é uma pegadinha de vestibular é só ler bem a questão e saber interpretar, é bem simples de resolvé-la basta multiplicar a área (que o problema nos dá ) pelos lados do hexágono ( 6 ),ou seja , 12 X 6 = 72cm² 
V = 12cm2
