POTENCIAÇÃO DE NÚMEROS COMPLEXOS

Os números complexos são identificados por z = a + bi, onde a é a parte real e b a parte imaginária. A letra i acompanha a parte imaginária e dependo do valor de sua potência ela irá assumir um valor que irá facilitar vários cálculos.

i ⁰ = 1, pois todo número ou letra elevando à zero é um.

i ¹ = i, pois todo número elevado a 1 é ele mesmo.

i ² = -1, a partir dessa potência que as outras irão derivar, veja:

i ³ = i² . i = -1 . i = - i

i ⁴ = i² . i² = -1 . (-1) = 1

i ⁵ = i⁴ . i = 1 . i = i

i ⁶ = i⁴ . i² = 1 . (-1) = -1.

i ⁷ = i⁴ . i³ = 1 . (-i) = - i. E assim por diante.

Para descobrir, por exemplo, qual era o valor da potência i²⁴³, basta observar o seguinte: nas potências acima elas repetem-se de 4 em 4, então basta dividirmos 243 por 4, o resto será 3 então i²⁴³ será o mesmo que i³, portanto i²⁴³ = - i.

Podemos concluir que iⁿ = i^r, onde r é o resto da divisão.

Potências de Números Imaginários

Exemplo de Potência de Número Imaginário

á vimos que o cálculo de potências de números reais com expoente natural é realizado através de uma multiplicação em que todos os fatores são iguais à base e em quantidade igual ao expoente natural.

Veja que a potência abaixo é o resultado de uma multiplicação com 3 fatores iguais a 5:

Esta outra potência é resultado de uma multiplicação contendo 4 fatores iguais a 7:

No caso de potências de números complexos com expoente natural o procedimento é o mesmo:

Se já é trabalhoso realizar diversas multiplicações no caso dos números reais, imagine realizar as multiplicações acima, que contém quatro números complexos. A multiplicação de números complexos é realizada tal qual a multiplicação de polinômios.

Quando a parte imaginária de um número complexo é nula, temos um número número real e o cálculo da potência é realizado como vimos no primeiro exemplo deste artigo:

Quando temos um número imaginário puro, isto é, quando a parte real de um número complexo é nula, o cálculo da potência pode ser realizado como no seguinte exemplo:

Note que na expressão acima temos que i⁵ é igual a i¹, pois o resto da divisão de 5 por 4 é igual a 1. Se você não sabe o porquê de tal igualdade, por favor, acesse o artigo potências da unidade imaginária.

Números complexos cujas partes real e imaginária não são nulas, são números imaginários.

De forma alternativa podemos calcular potências de números imaginários com expoente natural, recorrendo ao Binômio de Newton.

Como já estudamos no referido artigo, segundo o método de Isaac Newton o desenvolvimento de (a + b)ⁿ com 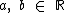 e 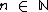 é dado por:

Vejamos como realizar o cálculo da potência (-3 - 5i)⁴ segundo o método do Binômio de Newton:

Substituindo a, b e n por -3, -5 e 4, respectivamente, na sentença do desenvolvimento de (a + b)ⁿ, segundo o método de Isaac Newton, temos:

Observe que todos os números binomiais possuem numerador igual a 4 e os denominadores vão de 0 a 4, do número binomial 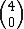 ao número binomial .

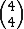Assim como nas frações, o número superior de um número binomial é chamado numerador e o inferior é odenominador.

Note ainda que o expoente dos fatores -3, a parte real do número complexo, começa em 4, o expoente da potência, e decresce até 0.

Já o expoente dos fatores -5i, a parte imaginária do número complexo, ao contrário, começa em 0 e cresce até 4.

Os números binomiais podem ser calculados segundo a fórmula da combinação simples:

No entanto para agilizarmos o desenvolvimento deste exemplo, podemos aplicar algumas propriedades que vimos no estudo dos números binomiais.

Como 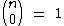,  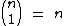e 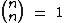, temos que:

Precisamos ainda calcular 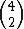 e .

 é 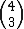obtido através da fórmula da combinação simples:

No caso do número binomial 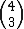, vamos recorrer a uma outra propriedade.

No estudo dos números binomiais aprendemos que 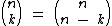, então podemos concluir que:

Substituindo cada número binomial por seu respectivo valor e desenvolvendo a expressão, temos:

Para a conclusão dos cálculos, a partir deste ponto vamos utilizar os conhecimentos adquiridos sobre as potências da unidade imaginária: